Стр.25 Часть 1 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1


Решение #2












Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
4. Дорогу от школы до автовокзала длиной 915 м покрыли асфальтом за неделю. В перзые 3 дня покрывали по 12 5 м в день, а остальную часть дороги покрывали в течение четырёх дней, во все дни поровну. Сколько метров дороги покрывали асфальтом в каждый из последних четырёх дней?
5. Длина прямоугольника 24 см, а ширина — в 8 раз меньше. Найди плодэдь и периметр этого грямоугольника.
6. Среди данных углов найди прямые углы. Запиши их обозначения.
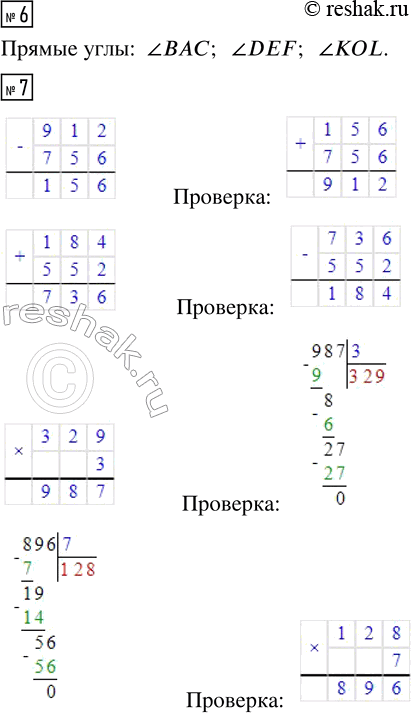
7. Выполни действия и сделай проверку.
912 - 756 184 + 552 329 · 3 896 : 7
8. Поставь вместо кружков знаки действий только первой (или только второй) ступени так, чтобы получились верные записи.
8 6 2 3 4 = 2 8 6 2 3 4 = 9
8 6 2 3 4 = 7 8 6 2 3 4 = 8
4.
Для того, чтобы найти, сколько метров дороги покрывали асфальтом в каждый из последних четырёх дней, необходимо сначала найти количество метров дороги, которое покрыли за последние четыре дня, а затем разделить это число на 4.
Для того, чтобы найти, сколько метров дороги покрыли за первые 3 дня, необходимо умножить количество метров, которое покрывали в день, на 3 дня.
То есть, необходимо умножить 125 на 3.
125
3
375
Пишу: 125•3.
Умножаю единицы: 5•3=15. 15 ед. – это 1 дес. 5 единиц; пишу 5 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Умножаю десятки: 2•3=6, да ещё 1.
6+1=7. Пишу 7 под десятками.
Умножаю сотни: 1•3=3. Пишу 3 под сотнями.
Читаю ответ: 375.
Значит, 375 метров дороги покрыли за первые 3 дня.
Для того, чтобы узнать, сколько метров дороги покрыли за 4 последних дня, необходимо количество метров дороги, которое покрыли за 3 дня, вычесть из длины всей дороги.
915
375
540
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 915-375.
Вычитаем единицы: 5-5=0. Пишу 0 под единицами.
Вычитаем десятки: из 1 десятка нельзя вычесть 7 десятков, поэтому возьмём из 9 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 9). 10+1=11.
Вычтем: 11-7=4. Пишем 4 под десятками.
Вычитаем сотни: было 9 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 8 сотен.
Вычтем: 8-3=5. Пишем 5 под сотнями.
Читаем ответ: 540.
Значит, 540 м дороги покрыли за оставшиеся 4 дня.
540 4
4 135
14
12
20
20
0
Пишем: 540:4.
Первое неполное делимое – 5 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 5 на 4, получу 1 - столько сотен будет в частном.
Умножу 4 на 1, получу 4 - столько сотен разделили.
Вычту: 5-4=1 – столько сотен осталось разделить.
Делю десятки: 1 сотня 4 десятка – это 14 десятков.
Разделю 14 на 4, получу 3 - столько десятков будет в частном.
Умножу 4 на 3, получу 12 - столько десятков разделили.
Вычту: 14-12=2 – столько десятков осталось разделить.
Делю единицы: 2 десятка 0 единиц – это 20 единиц.
Разделю 20 на 4, получу 5 - столько единиц будет в частном.
Умножу 4 на 5, получу 20 - столько единиц разделили.
Вычту: 20-20=0 – единицы разделили все.
Читаю ответ: 135.
Значит, 135 метров дороги покрывали асфальтом в каждый из последних четырёх дней.
Ответ: 135 метров.
5.
Запишем краткое условие задачи.
Длина прямоугольника - 24 см
Ширина прямоугольника - ?, в 8 раз меньше
Площадь прямоугольника - ? ?см?^2
Периметр прямоугольника - ? см
Фраза «в 8 раз меньше», подсказывает нам, что для того, чтобы найти ширину прямоугольника, необходимо его длину разделить на 8. То есть, необходимо разделить 24 см на 8.
24:8=3 (см) – ширина прямоугольника.
Для того, чтобы найти площадь прямоугольника, необходимо умножить его длину на ширину.
S=a•b, где S – площадь, a и b – смежные стороны.
24
3
72
Пишу: 24•3.
Умножаю единицы: 4•3=12. 12 ед. – это 1 дес. 2 ед.; пишу 2 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Умножаю десятки: 2•3=6, да ещё 1.
6+1=7. Пишу 7 под десятками.
Читаю ответ: 72.
Значит, площадь прямоугольника составляет 72 ?см?^2.
Периметр многоугольника равен сумме длин его сторон.
Заметим, что в сумме 24=8+24+8, два раза повторяется сумма слагаемых 24+8. Значит, мы можем 24+8 умножить на 2.
P=(24+8)•2=24•2+8•2=(20+4)•2+16=
=20•2+4•2+16=40+8+16=40+24=64 (см).
Значит, периметр прямоугольника равен 64 см.
Ответ: 72 ?см?^2; 64 см.
6.
Для того, чтобы определить с помощью чертёжного треугольника является угол прямым или нет, необходимо приложить одну из сторон прямого угла к стороне данного угла так, чтобы вершины углов совпали. Если при этом другая сторона данного угла окажется на стороне треугольника, то этот угол прямой. Если другая сторона окажется внутри треугольника или вне треугольника, то этот угол непрямой.
На рисунке мы видим 5 различных углов. Для того, чтобы узнать, какой из заданных углов прямой, приложим к каждому из них чертёжный треугольник.
Так как стороны угла ABC лежат на сторонах чертёжного треугольника, то угол ABC - прямой.
Так как сторона MP угла MPR лежит вне чертёжного треугольника, то угол MPR - непрямой.
Так как стороны угла KOL лежат на сторонах чертёжного треугольника, то угол KOL - прямой.
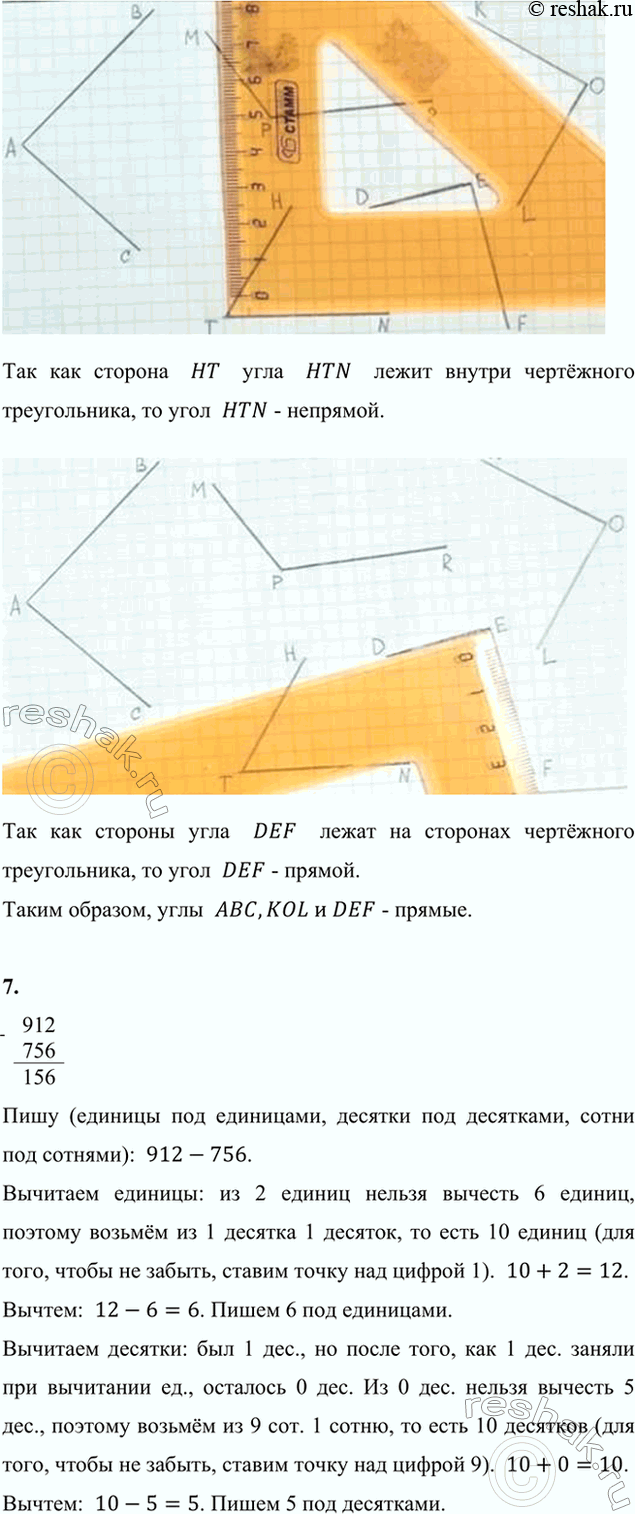
Так как сторона HT угла HTN лежит внутри чертёжного треугольника, то угол HTN - непрямой.
Так как стороны угла DEF лежат на сторонах чертёжного треугольника, то угол DEF - прямой.
Таким образом, углы ABC,KOL и DEF - прямые.
7.
912
756
156
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 912-756.
Вычитаем единицы: из 2 единиц нельзя вычесть 6 единиц, поэтому возьмём из 1 десятка 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 1). 10+2=12.
Вычтем: 12-6=6. Пишем 6 под единицами.
Вычитаем десятки: был 1 дес., но после того, как 1 дес. заняли при вычитании ед., осталось 0 дес. Из 0 дес. нельзя вычесть 5 дес., поэтому возьмём из 9 сот. 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 9). 10+0=10.
Вычтем: 10-5=5. Пишем 5 под десятками.
Вычитаем сотни: было 9 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 8 сотен.
Вычтем: 8-7=1. Пишем 1 под сотнями.
Читаем ответ: 156.
Для того, чтобы проверить правильность выполнения вычитания, можно к вычитаемому прибавить разность. Если получится уменьшаемое, то действие выполнено верно.
756
156
912
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 756+156.
Складываем единицы: 6+6=12. 12 ед. – это 1 дес. 2 ед.; пишу 2 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываем десятки: 5+5=10, да ещё 1.
10+1=11. 11 дес. – это 1 сотня 1 десяток; пишу 1 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываем сотни: 7+1=8, да ещё 1.
8+1=9. Пишу 9 под сотнями.
Читаю ответ: 912.
Так как при сложении вычитаемого и разности мы получили уменьшаемое, то действие выполнено верно.
184
552
736
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 184+552.
Складываем единицы: 4+2=6. Пишу 6 под единицами.
Складываем десятки: 8+5=13. 13 дес. – это 1 сотня 3 десятка; пишу 3 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываем сотни: 1+5=6, да ещё 1.
6+1=7. Пишу 7 под сотнями.
Читаю ответ: 736.
Для того, чтобы проверить правильность сложения двух слагаемых, из суммы вычитают одно из слагаемых. Если получится другое слагаемое, то действие выполнено верно.
736
552
184
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 736-552.
Вычитаем единицы: 6-2=4. Пишем 4 под единицами.
Вычитаем десятки: из 3 десятков нельзя вычесть 5 десятков, поэтому возьмём из 7 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 7). 10+3=13.
Вычтем: 13-5=8. Пишем 8 под десятками.
Вычитаем сотни: было 7 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 6 сотен.
Вычтем: 6-5=1. Пишем 1 под сотнями.
Читаем ответ: 184.
Так как при вычитании второго слагаемого из суммы мы получили первое слагаемое, то действие выполнено верно.
329
3
987
Пишу: 329•3.
Умножаю единицы: 9•3=27. 27 ед. – это 2 дес. 7 единиц; пишу 7 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 2•3=6, да ещё 2.
6+2=8. Пишу 8 под десятками.
Умножаю сотни: 3•3=9. Пишу 9 под сотнями.
Читаю ответ: 987.
Для того, чтобы проверить правильность умножения двух чисел, произведение делят на один из множителей. Если получится другой множитель, то действие выполнено верно.
987 3
9 329
8
6
27
27
0
Пишем: 987:3.
Первое неполное делимое – 9 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 9 на 3, получу 3 - столько сотен будет в частном.
Умножу 3 на 3, получу 9 - столько сотен разделили.
Вычту: 9-9=0 – сотни разделили все.
Делю десятки: разделю 8 на 3, получу 2 - столько десятков будет в частном.
Умножу 3 на 2, получу 6 - столько десятков разделили.
Вычту: 8-6=2 – столько десятков осталось разделить.
Делю единицы: 2 десятка 7 единиц – это 27 единиц.
Разделю 27 на 3, получу 9 - столько единиц будет в частном.
Умножу 3 на 9, получу 27 - столько единиц разделили.
Вычту: 27-27=0 – единицы разделили все.
Читаю ответ: 329.
Так как при делении произведения на второй множитель, мы получили первый множитель, то действие выполнено верно.
896 7
7 128
19
14
56
56
0
Пишем: 896:7.
Первое неполное делимое – 8 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 8 на 7, получу 1 - столько сотен будет в частном.
Умножу 7 на 1, получу 7 - столько сотен разделили.
Вычту: 8-7=1 – столько сотен осталось разделить.
Делю десятки: 1 сотня 9 десятков – это 19 десятков.
Разделю 19 на 7, получу 2 - столько десятков будет в частном.
Умножу 7 на 2, получу 14 - столько десятков разделили.
Вычту: 19-14=5 – столько десятков осталось разделить.
Делю единицы: 5 десятков 6 единиц – это 56 единиц.
Разделю 56 на 7, получу 8 - столько единиц будет в частном.
Умножу 7 на 8, получу 56 - столько единиц разделили.
Вычту: 56-56=0 – единицы разделили все.
Читаю ответ: 128.
Для того, чтобы проверить правильность выполнения деления, можно делитель умножить на частное. Если получится делимое, то действие выполнено верно.
128
7
896
Пишу: 128•7.
Умножаю единицы: 8•7=56. 56 ед. – это 5 дес. 6 единиц; пишу 6 под единицами, а 5 десятков запомню и прибавлю к десяткам.
Умножаю десятки: 2•7=14, да ещё 5.
14+5=19. 19 десятков – это 1 сотня 9 десятков; пишу 9 под десятками, а 1 сотню запомню и прибавлю к сотням.
Умножаю сотни: 1•7=7, да ещё 1.
7+1=8. Пишу 8 под сотнями.
Читаю ответ: 896.
Так как при умножении делителя на частное, мы получили делимое, то действие выполнено верно.
8.
Если в выражении нет скобок, и оно содержит действия только одной ступени: сложение и вычитание (или умножение и деление), то их выполняют по порядку слева направо.
Подумаем, как расставить знаки вместо кружков в первом выражении.
1 2 3 4
8 * 6 * 2 * 3 * 4=2
Для того, чтобы определить верные знаки, необходимо выполнить обратные действия.
Выполнив первые три действия, мы получим какое-то неизвестное число, далее это число либо умножают на 4, либо делят на 4, либо прибавляют 4, либо вычитают 4 и получают число 2. Но не существует такого числа, к которому можно прибавить 4 и получить 2, значит, сложение в четвёртом действии отпадает. Также не существует числа, которое можно умножить на 4 и получить число 2. Значит, операция умножения в четвёртом действии также отпадает. Остаётся либо вычитание, либо деление.
Для того, чтобы проверить правильность выполнения вычитания, можно к вычитаемому прибавить разность. Если получится уменьшаемое, то действие выполнено верно.
Проверим операцию вычитания в четвёртом действии.
Если вычитаемое 4, то 2 – разность. Значит, 2=4=6.
То есть 8 * 6 * 2 * 3-4=6-4=2.
Подумаем, какой знак стоит вместо кружка в третьем действии.
Так как мы выбрали вычитание, а по условию задачи выражение содержит действия только одной ступени, то в третьем действии число 3 либо прибавляют к какому-то числу и получают 6, либо вычитают из какого-то числа и получают 6.
Проверим вычитание в третьем действии.
Так как 3 – вычитаемое, а 6 – разность, то 3+6=9 - результат первых двух действий.
То есть 8 * 6 * 2-3-4=9-3-4=2.
Подумаем, какой знак стоит вместо кружка во втором действии.
Во втором действии число 2 либо прибавляют к какому-то числу и получают 9, либо вычитают из какого-то числа и получают 9.
Так как 2 – вычитаемое, а 9 – разность, то 2+9=11 – результат первого действия.
То есть 8 * 6-2-3-4=11-2-3-4=2.
Подумаем, какой знак стоит вместо кружка в первом действии.
В первом действии число 6 либо прибавляют к 8 и получают 11, либо вычитают из 8 и получают 11, но это невозможно, так как 8-6=2, а
8+6=14.
Значит, знаки в действиях расставлены неверно.
Вспомним, как проверить правильность сложения двух слагаемых.
Для того, чтобы проверить правильность сложения двух слагаемых, из суммы вычитают одно из слагаемых. Если получится другое слагаемое, то действие выполнено верно.
Проверим операцию сложения во втором действии.
Так как 2 – второе слагаемое, а 9 – сумма, то 9-2=7 - результат первого действия. Но, мы выяснили, что результат первого действия – это число 2 или число 14. Значит, знаки снова расставлены неверно.
Вернёмся к третьему действию и проверим операцию сложения.
Так как 3 – второе слагаемое, а 6 – сумма, то 6-3=3 - результат первых двух действия.
То есть 8 * 6 * 2+3-4=3+3-4=2.
Подумаем, какой знак теперь стоит вместо кружка во втором действии.
Во втором действии число 2, либо прибавляют к какому- то числу и получают 3, либо вычитают из какого-то числа и получают 3.
Проверим вычитание во втором действии.
Так как 2 – вычитаемое, а 3 разность, то 3+2=5 - результат первого действия. Но, мы выяснили, что результат первого действия – это число 2 или число 14. Значит, знаки снова расставлены неверно.
Проверим сложение во втором действии.
Так как 2 – второе слагаемое, а 3 – сумма, то 3-2=1 - результат первого действия. Но, мы выяснили, что результат первого действия – это число 2 или число 14. Значит, знаки снова расставлены неверно.
Методом перебора мы рассмотрели все возможные действия первой ступени и не получили ни одного верного решения. Значит, в первом выражении используются действия второй ступени.
Мы выяснили, что в четвёртом действии стоит либо вычитание либо деление. Затем мы выяснили, что вычитание – неверно, значит, в четвёртом действии стоит деление.
Для того, чтобы проверить правильность выполнения деления, можно делитель умножить на частное. Если получится делимое, то действие выполнено верно.
Проверим деление в четвёртом действии.
Если 4 – делитель, то 2 – частное, значит, 2•4=8 - делимое.
То есть 8 * 6 * 2 * 3:4=8:4=2.
Так как мы выбрали деление, а по условию задачи выражение содержит действия только одной ступени, то в третьем действии какое-то неизвестное число либо делят на 3 и получают 8, либо умножают на 3 и получают 8. Но нет такого числа, которое можно умножить на 3 и получить 8, значит, какое-то число делят на 3 и получают 8.
Так как 3 – делитель, а 8 – частное, то 3•8=24 - делимое.
То есть 8 * 6 * 2:3:4=24:3:4=8:4=2.
Во втором действии какое-то неизвестное число либо делят на 2 и получают 24, либо умножают на 2 и получают 24.
Для того, чтобы проверить правильность умножения двух чисел, произведение делят на один из множителей. Если получится другой множитель, то действие выполнено верно.
Сумму на число можно разделить так, разделить каждое слагаемое суммы на число и найти сумму полученных частных.
Проверим операцию умножения во втором действии.
Так как 2 – второй множитель, а 24 – произведение, то 24:2=(20+4) :2=20:2+4:2=10+2=12.
То есть 8 * 6•2:3:4=12•2:3:4=24:3:4=8:4=2.
В первом действии число 8 либо умножают на 6 и получают 12, либо делят на 6 и получают 12, но это невозможно, так как 8•6=48, а 8:6=1 (ост. 2).
Так как 8 не делится без остатка на 6, то в первом действии число 8 точно умножают на 6 и получают в первом действии число 48, а знаки в следующих действиях расставлены неверно.
Сумму на число можно умножить, если умножить каждое слагаемое суммы на число и полученные произведения сложить.
Проверим операцию деления во втором действии.
Так как 2 – делимое, а 24 частное, то 24•2=(20+4)•2=20•2+4•2=40+8=48 - делимое. А мы выяснили, что результата первого действия и есть число 48.
То есть 8•6:2:3:4=48:2:3:4=24:3:4=8:4=2 – верно.
Методом перебора и проверки каждого действия, рассуждая аналогично первого выражения, мы придём к тому, что во втором выражении используются действия первой ступени, то есть сложение и вычитание.
Вычисления одним выражением будут выглядеть так:
8-6-2+3+4=2-2+3+4=0+3+4=3+4=7.
Запишем знаки действий вместо кружков во втором выражении.
8-6-2+3+4=7.
Методом перебора и проверки каждого действия, рассуждая аналогично первого выражения, мы придём к тому, что в третьем выражении используются действия первой ступени, то есть сложение и вычитание.
Вычисления одним выражением будут выглядеть так:
8+6+2-3-4=14+2-3-4=16-3-4=13-4=9.
Запишем знаки действий вместо кружков во втором выражении.
8+6+2-3-4=9.
Методом перебора и проверки каждого действия, рассуждая аналогично первого выражения, мы придём к тому, что в четвёртом выражении используются действия второй ступени, то есть умножение и деление.
Вычисления одним выражением будут выглядеть так:
8•6•2:3:4=48•2:3:4=96:3:4=32:4=8.
Запишем знаки действий вместо кружков во втором выражении.
8•6•2:3:4=8.
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.