Упражнение 4 ГДЗ Перышкин 9 класс (Физика)
Решение #1

Решение #2


Рассмотрим вариант решения задания из учебника Перышкин 9 класс, Дрофа:
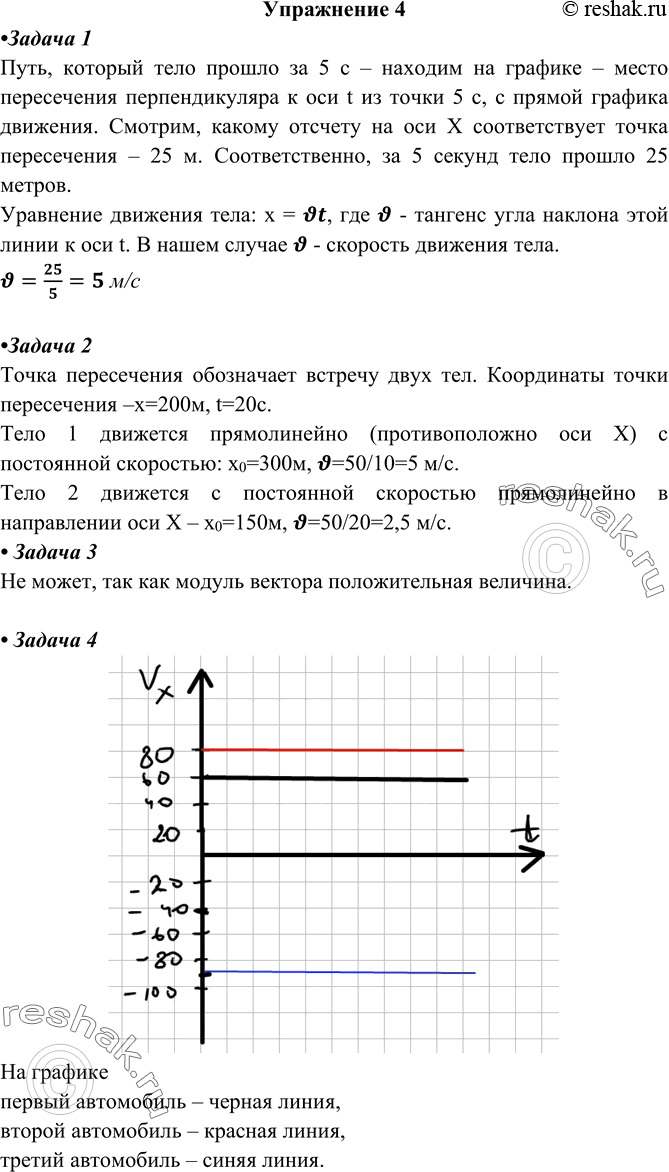
1. Тело движется вдоль оси X. Определите по графику движения (рис. 10) путь, пройденный телом за 5 с, и скорость движения тела. Запишите уравнение движения тела.
Путь, который тело прошло за 5 с – находим на графике – место пересечения перпендикуляра к оси t из точки 5 с, с прямой графика движения. Смотрим, какому отсчету на оси Х соответствует точка пересечения – 25 м. Соответственно, за 5 секунд тело прошло 25 метров.
Уравнение движения тела: x = ?t, где ? - тангенс угла наклона этой линии к оси t. В нашем случае ? - скорость движения тела.
2. Охарактеризуйте движение тел, графики движения которых показаны на рисунке 11. Что обозначает точка пересечения графиков и что по ней можно узнать?
Точка пересечения обозначает встречу двух тел. Координаты точки пересечения –х=200м, t=20c.
Тело 1 движется прямолинейно (противоположно оси Х) с постоянной скоростью: х0=300м, V=50/10=5 м/с.
Тело 2 движется с постоянной скоростью прямолинейно в направлении оси Х – х0=150м, V=50/20=2,5 м/с.
3. Может ли график зависимости модуля вектора скорости от времени располагаться под осью Ot (т. е. в об-пасти отрицательных значений оси скорости)?
Не может, так как модуль вектора положительная величина.
4. Постройте графики зависимости проекций векторов скорости от времени для трех автомобилей, движущихся прямолинейно и равномерно, если два из них едут в одном направлении, а третий — навстречу им. Скорость первого автомобиля равна 60 км/ч, второго — 80 км/ч, а третьего — 90 км/ч.
На графике
первый автомобиль – черная линия,
второй автомобиль – красная линия,
третий автомобиль – синяя линия.
5. Координата тела, движущегося прямолинейно и равномерно, изменяется по закону х = 6 + 3t (м). Постройте графики зависимости от времени координаты и пути. Сравните полученные графики.
Строим график x = 6+3t
Пусть t1 = 0 c, тогда x1 = 6 м
Пусть t2 = 1 c, тогда x2 = 9 м
Графиком данной функции является прямая линия, то проводим прямую, проходящую через точки, которые получили выше.
2)
Запишем заданное уравнение в виде:
x0 = x(0) = 6
x = x(t) = 6+3t
S = x - x0
S = 6 + 3t - 6
S = 3t.
Строим график. Он выходит из начала координат.
Делаем вывод о том, что графики параллельны, что говорит о постоянной скорости тела. V = 3 м/с
1. Из рисунка 10 следует, что: - Начальная координата тела равна: x0=0; - Координата тела через t=5 секунд равна: x1=25 м;
1) Путь, пройденный телом за 5 секунд равен: sx=|x1-x0 |=|25-0|=25 м;
2) Скорость движения тела равна: vx=sx/t=25/5=5 м/с;
3) Уравнение движения тела: x=x0+vx t=0+5t=5t; Ответ: sx=25 м; vx=5 м/с; x=5t.
2. По рисунку 11 определим, что графики движения тел представляют собой прямые, следовательно:
1) Тело I движется: - Прямолинейно (без изменения направления); - Равномерно (без ускорения); - Функция убывает, значит тело движется к точке отсчета; - Начальная координата тела равна: x0=300 м; - Скорость движения тела составляет: vx1=(x1-x0)/t=(200-300)/20=-100/20=-5 м/с;
2) Тело II движется: - Прямолинейно (без изменения направления); - Равномерно (без ускорения); - Функция возрастает, значит тело движется от точки отсчета; - Начальная координата тела равна: x0=150 м; - Скорость движения тела составляет: vx2=(x1-x0)/t=(200-150)/20=50/20=2,5 м/с;
3) Точка пересечения графиков обозначает встречу данных тел; По этой точке можно узнать координату (x) и время (t) встречи тел: x=200 м; t=20 с; 3.
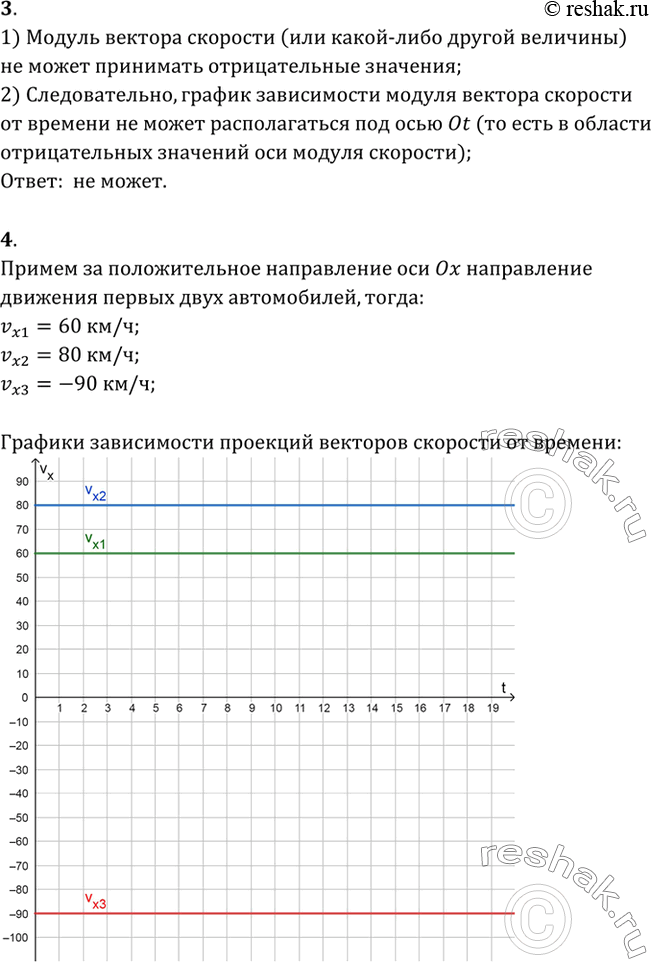
1) Модуль вектора скорости (или какой- либо другой величины) не может принимать отрицательные значения;
2) Следовательно, график зависимости модуля вектора скорости от времени не может располагаться под осью Ot (то есть в области отрицательных значений оси модуля скорости); Ответ: не может.
4. Примем за положительное направление оси Ox направление движения первых двух автомобилей, тогда: vx1=60 км/ч; vx2=80 км/ч; vx3=-90 км/ч; Графики зависимости проекций векторов скорости от времени: 5. Координата тела, движущегося прямолинейно и равномерно, изменяется по закону x=6+3t (м);
1) Координаты тела: x(0)=6+3•0=6+0=6 м; x(1)=6+3•1=6+3=9 м; x(2)=6+3•2=6+6=12 м;
2) Пройденный телом путь: s(0)=0; s(1)=x(1)-x(0)=9-6=3 м; s(2)=x(2)-x(0)=12-6=6 м;
3) Графики зависимости от времени координаты (I) и пути (II): Ответ: данные графики параллельны, при этом график зависимости пути от времени лежит на шесть единиц ниже, чем график зависимости координаты от времени.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







