Задание 18 ГДЗ Рабочая тетрадь Босова 7 класс (Информатика)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2016)

Решение #4 (Учебник 2016)


Рассмотрим вариант решения задания из учебника Босова 7 класс, Просвещение:
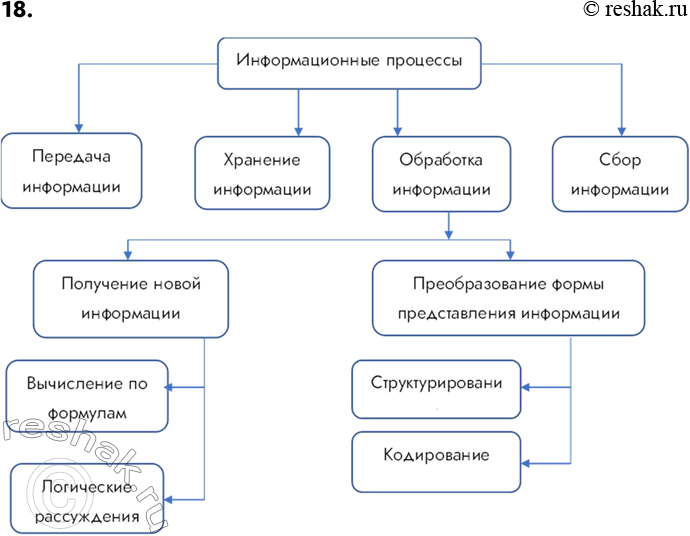
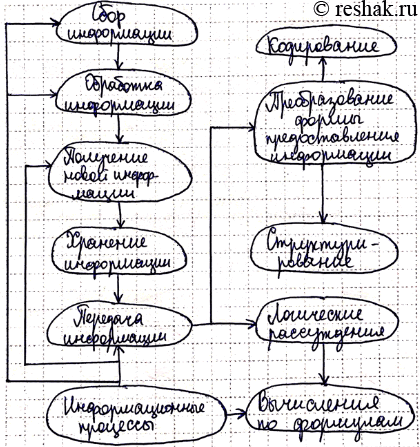
18. Постройте граф, отражающий отношения между следующими понятиями: информационные процессы, сбор информации, обработка информации, хранение информации, передача информации, получение новой информации, преобразование формы представления информации, вычисление по формулам, структурирование, логические рассуждения, кодирование.
18. Играют двое. Первый участник игры называет произвольное целое число, не превышающее десяти. Второй игрок прибавляет к названному числу своё целое число, тоже не превышающее десяти, и сообщает полученную сумму. К этой сумме первый игрок также прибавляет произвольное целое число, не превышающее десяти, и сообщает новую сумму. К новой сумме второй прибавляет число и т. д. до тех пор, пока окончательной суммой не окажется число 100. Выигрывает тот, кто первым достигнет 100. Как должен действовать первый игрок, чтобы выиграть?
Не превышающее 10, это числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Чтобы первый игрок смог выиграть, надо чтобы второй игрок не смог набрать 100 на последнем своем ходе, но, в то же время, создал ситуацию, когда следующим ходом выигрывает первый игрок.
Если первый игрок сделает 89 на последнем ходе, второму ничего не остается, как прибавить любое число (не более 10), чтобы позволить следующим ходом выиграть первому игроку.
Чтобы второй игрок не смог первым набрать 89, первый игрок должен дать ход меньше 89 на 11 (как и на последнем ходе), т.е. 78. И так далее на уменьшение. Предыдущий ход должен быть 67, перед эти ход 56.
Если просматривать все выигрышные ходы первого игрока, то последовательно должны достигаться следующие результаты – 1, 12, 23, 34, 45, 56, 67, 78, 89, 100. Иначе, он должен выполнять условие, что сумма ходов его и второго игрока на каждом шаге должна быть всегда 11!
Похожие решебники
Популярные решебники 7 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.








