Задание 14 ГДЗ Рабочая тетрадь Босова 7 класс (Информатика)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2016)
Решение #4 (Учебник 2016)
Рассмотрим вариант решения задания из учебника Босова 7 класс, Просвещение:
14. В шахматном турнире принимали участие шесть игроков из разных городов России: Воркуты, Иркутска, Саратова, Тюмени, Уфы и Рязани. Всего было сыграно пять туров, по три партии в каждом туре.
В первом туре Александр играл с представителем Воркуты, уфимец — с Николаем, а Геннадий — с Михаилом. Во втором туре Денис играл с представителем Тюмени, а шахматист из Воркуты — с Николаем. В третьем туре Михаил играл с иркутянином.
Кто из игроков представлял какой город, если в итоге Николай занял первое место, Геннадий и иркутянин поделили 2-е и 3-е места, Денис был четвёртым, а Семён и саратовец поделили 5-е и 6-е места?
Александр не из Воркуты, и не из Уфы. Николаев тоже не из Уфы и не из Воркуты, также как и Геннадий с Михаилом, так как они играли все в первом туре.
Николаев не из Тюмени.
Денис и Семен могут быть или из Воркуты, или из Уфы.
Денис не из Тюмени и не из Воркуты, Михаил не из Иркутска.
Получается Денис из Уфы, а Семен из Воркуты
Николаев, Геннадий не из Иркутска, и не из Саратова.
Из Иркутска может быть только Александр, так как у всех остальных прочерк, тогда Михал Может быть только из Саратова.
Далее, по таблице видно, Николаев из Рязани, а Геннадий из Уфы.
Ответ: Александр из Иркутска, Николай из Рязани, Геннадий из Тюмени, Михаил из Саратова, Денис из Уфы, Семен из Воркуты.
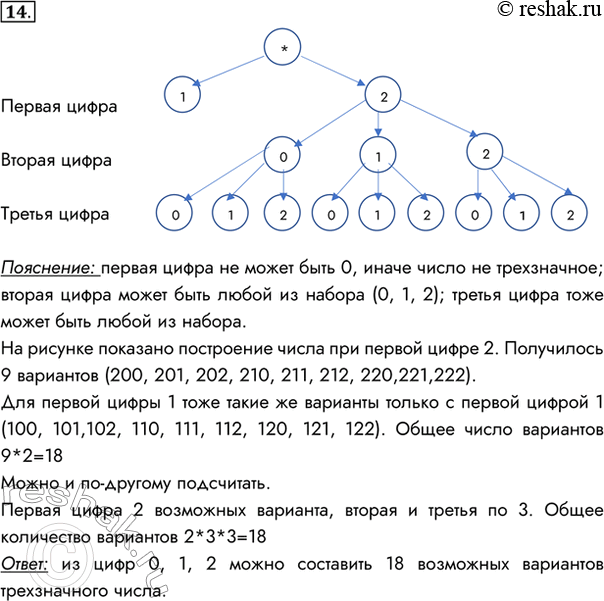
14. Какие трёхзначные числа можно составить из цифр О, 1, 2? Решите задачу, достроив дерево возможных вариантов.
Первая цифра
Вторая цифра
Третья цифра
Пояснение: первая цифра не может быть 0, иначе число не трехзначное; вторая цифра может быть любой из набора (0, 1, 2); третья цифра тоже может быть любой из набора.
На рисунке показано построение числа при первой цифре 2. Получилось 9 вариантов (200, 201, 202, 210, 211, 212, 220,221,222).
Для первой цифры 1 тоже такие же варианты только с первой цифрой 1 (100, 101,102, 110, 111, 112, 120, 121, 122). Общее число вариантов 9*2=18
Можно и по-другому подсчитать.
Первая цифра 2 возможных варианта, вторая и третья по 3. Общее количество вариантов 2*3*3=18
Ответ: из цифр 0, 1, 2 можно составить 18 возможных вариантов трехзначного числа.
Похожие решебники
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением