Упр.776 ГДЗ Колягин Ткачёва 9 класс (Алгебра)
Решение #1
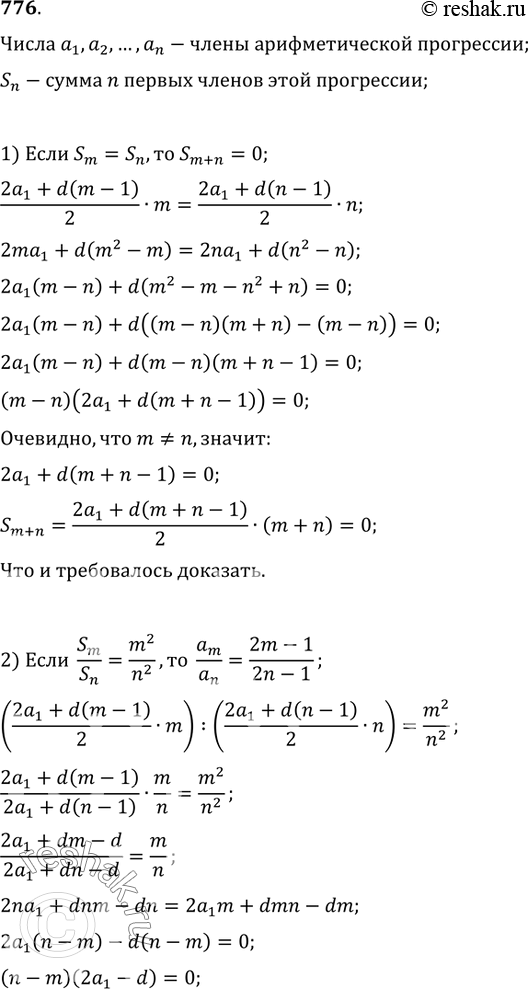
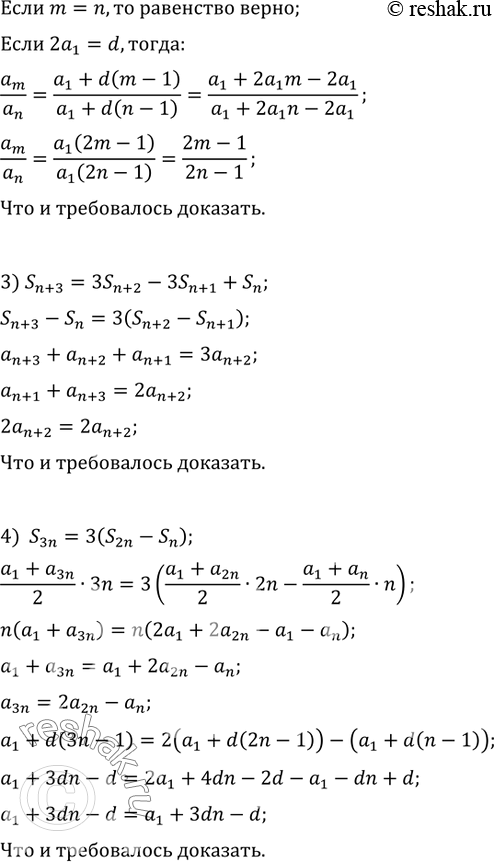
Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 9 класс, Просвещение:
776. Пусть числа a_1, a_2, ..., a_n, ... являются последовательными членами арифметической прогрессии, S_n — сумма n первых членов этой прогрессии. Доказать, что:
1) если S_m=S_n, то S_(m+n)=0; 2) S_(n+3)=3S_(n+2)-3S_(n+1)+S_n;
3) если S_m/S_n, то a_m/a_n=(2m-1)/(2n-1); 4) S_(3n)=3(S_(2n)-S_n).
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
