Упр.6.7 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
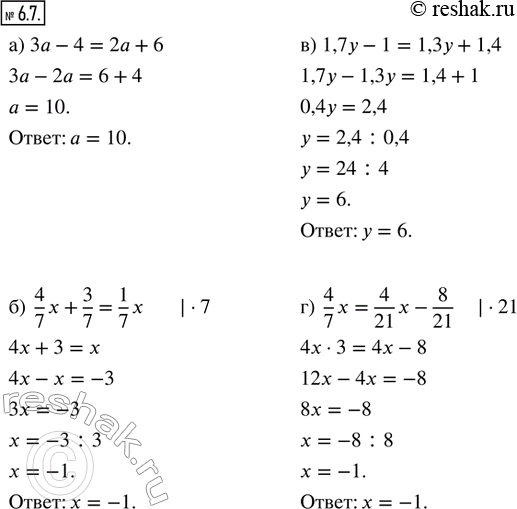
Решение #2 (Учебник 2023)
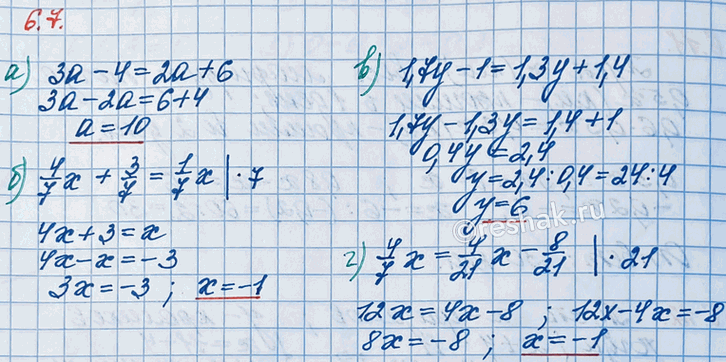
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Решите уравнение:
а) 3а - 4 = 2а + 6; в) 1,7y - 1 = 1,3у + 1,4:
б) 4/7 x + 3/7 = 1/7 x; г) 4/7 x = 4/21 x - 8/21.
Известно, что решить уравнение – значит найти все его корни или показать, что их нет вообще.
При этом учитываем то, что уравнения не изменяются:
- если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак, то есть при переносе слагаемого из левой части в правую или наоборот, необходимо поменять его знак на противоположный.
- если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
а) В уравнении 3a-4=2a+6 переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат, получим 3a-2a=4+6.
Далее приводим подобные слагаемые и получаем a=10.
б) В уравнении 4/7 x+3/7=1/7 x умножаем левую и правую части уравнения на 7, получим 7•(4/7 x+3/7)=7•1/7 x или
7•4/7 x+7•3/7=7•1/7 x
(7•4)/7 x+(7•3)/7=(7•1)/7 x , откуда 4x+3=x.
Переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат, получим 4x-x=-3.
Далее приводим подобные слагаемые и получаем 3x=-3.
Неизвестный множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим x=-3:3 или, выполнив деление, x=-1.
в) В уравнении 1,7y-1=1,3y+1,4 умножаем левую и правую части уравнения на 10, получим
10•(1,7y-1)=10•(1,3y+1,4) или
10•1,7y-10•1=10•1,3y+10•1,4, откуда, выполнив умножение, 17y-10=13y+14
Далее переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат, получим 17y-13y=10+14.
Далее приводим подобные слагаемые и получаем 4y=24.
Неизвестный множитель y.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим y=24:4 или, выполнив деление, x=6.
г) В уравнении 4/7 x=4/21 x-8/21 умножаем левую и правую части уравнения на 21, получим 21•4/7 x=21•(4/21 x-8/21) или
21•4/7 x=21•4/21 x-21•8/21
(21•4)/7 x=(21•4)/21 x-(21•8)/21
(3•7•4)/7 x=(21•4)/21 x-(21•8)/21 , откуда 12x=4x-8.
Переносим в левую часть уравнения все слагаемые, которые содержат неизвестную, а в правую, которые не содержат, получим 12x-4x=-8.
Далее приводим подобные слагаемые и получаем 8x=-8.
Неизвестный множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим x=-8:8 или, выполнив деление, x=-1.
Вычисления выполняем по следующим правилам:
- для того, чтобы умножить десятичную дробь на10, необходимо в этой дроби перенести запятую вправо на цифру.
- для того, чтобы найти частное двух чисел с разными знаками, необходимо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «-».
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением