Упр.2.78 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
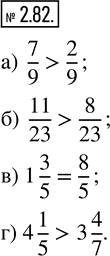
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
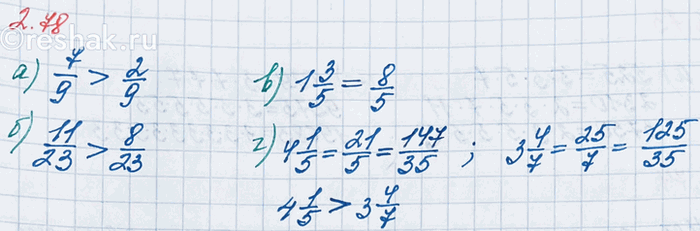
Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Сравните числа:
а) 7/9 и 2/9; б) 11/23 и 8/23; в) 1 3/5 и 8/5; г) 4 1/5 и 3 4/7.
а) Знаменатель дроби показывает, на сколько долей делят, а числитель – сколько таких долей взято.
Дроби 7/9 и 2/9 можно «показать» на примере пирога.
Представьте, что пирог разрезали на 9 равных частей (долей).
Семь таких частей – это дробь 7/9.
Две такие части – это дробь 2/9.
Таким образом, из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.
Значит, у дробей с одинаковыми знаменателями (число под дробной чертой) сравниваем числители (число над дробной чертой).
Например, 7/9 и 2/9.
Знаменатели этих дробей равны (число 9).
Числитель первой дроби число 7.
Числитель второй дроби число 2.
7>2, значит, 7/9>2/9
б) Сравнение проводим аналогично пункту а.
У дробей с одинаковыми знаменателями (число под дробной чертой) сравниваем числители (число над дробной чертой).
11/23 и 8/23.
Знаменатели этих дробей равны (число 23).
Числитель первой дроби число 11.
Числитель второй дроби число 8.
11>8, значит, 11/23>8/23
в) Первое число 1 3/5 представлено в смешанной записи (есть целая часть и дробная часть).
Второе число 8/5 является неправильной дробью, потому что числитель больше знаменателя.
Смешанное число можно представить в виде неправильной дроби.
Для этого нужно:
- умножить его целую часть на знаменатель дробной части 1•5
- к полученному произведению прибавить числитель дробной части 1•5+3
- записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения (1•5+3)/5.
Выполним действия в числителе и получим неправильную дробь (1•5+3)/5=8/5.
Это как раз число, которое стоит справа.
Получилось, что смешанное число 1 3/5 равно неправильной дроби 8/5.
Это и есть ответ 1 3/5=8/5.
г) 4 1/5 и 3 4/7
Обратим внимание на то, что в смешанной записи этих чисел целая часть первого числа (4) больше целой части второго числа (3).
Дробные части этих чисел являются правильными дробями (числитель меньше знаменателя).
Поэтому, дробные части не повлияют на окончательный результат сравнения, то есть
4 1/5>3 4/7
Разложение одного числа состоит из двух простых множителей, а другого — из трёх простых множителей. Будут ли эти числа равными?
«Разложите на множители» говорят вместо слов «представьте в виде произведения».
При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
Число, которое разлагается на 2 простых множителя, не может равняться числу, которое разлагается на 3 простых множителя.
Например, одно число разлагается на два простых множителя (2•3), другое число разлагается на три простых множителя (2•3•5).
(2•3) ? (2•3•5)
2•3=6
2•3•5=6•5=30
6 не равно 30
2•3 не равно 2•3•5
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









