Упр.2.475 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
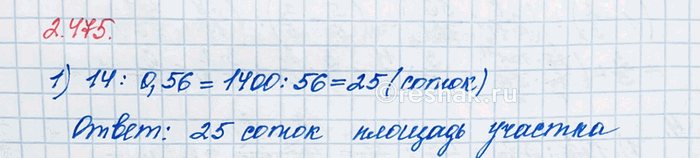
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
На приусадебном участке 14 соток занимает огород, что составляет 0,56 всего участка. Чему равна площадь приусадебного участка?
По условию задачи, огород занимает 14 соток всего участка, что составляет 0,56 всего участка.
Для того, чтобы найти число по данному значению его дроби, необходимо это значение разделить на дробь.
Для того, чтобы разделить десятичную дробь на десятичную, необходимо перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе; выполнить деление на натуральное число.
Тогда, площадь всего приусадебного участка составляет
14:0,56=1400:56=25 соток.
Ответ: 25 соток.
Снегоуборочная машина до обеда расчистила участок, составляющий 5/7 от длины участка, расчищенного ею после обеда. Сколько километров дороги она расчистила за весь день, если участок, расчищенный после обеда, оказался на 14 км больше участка, расчищенного до обеда?
Решаем задачу при помощи уравнения.
Пусть снегоуборочная машина после обеда расчистила x км длины участка.
Тогда, до обеда было расчищено 5/7 x км участка, так как до обеда машина расчистила участок, составляющий 5/7 от длины участка, расчищенного ею после обеда, а, чтобы найти дробь от числа, необходимо умножить число на эту дробь.
При этом участок, расчищенный после обеда, оказался на 14 км больше участка, расчищенного до обеда.
Следовательно, можно составить следующее уравнение
x-5/7 x=14 , или, учитывая то, что при умножении единицы на любое число, получим равное ему число, можно записать
1•x-5/7 x=14
Далее преобразуем полученное уравнение, используя распределительное свойство умножения относительно вычитания, то есть выносим одинаковый множитель x за скобки, получим
(1-5/7)x=14
Для того, чтобы найти разность двух смешанных чисел, необходимо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Тогда, выполнив вычитание в скобках, получим
(7/7-5/7)x=14
(7-5)/7 x=14
2/7 x=14
В полученном уравнении неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=14:2/7
Для того, чтобы разделить натуральное число на обыкновенную дробь, необходимо делимое умножить на число, обратное делителю, то есть у делителя поменять местами числитель и знаменатель, получим
x=14•7/2
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений, тогда
x=(14•7)/2
Или, выполнив сокращение, x=(2•7•7)/2
x=49/1
Дробь, у которой в знаменателе стоит единица, равна числителю.
Значит, x=49.
Следовательно, после обеда машина расчистила 49 км участка.
Участок, расчищенный после обеда, оказался на 14 км больше участка, расчищенного до обеда, то есть до обеда расчищено на 14 км меньше, участка, расчищенного после обеда, получим, что до обеда было расчищено
49-14=35 км участка.
Тогда, за весь день машина расчистила 35+49=84 км.
Ответ: 84 км.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением