Упр.2.166 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)

Решение #1 (Учебник 2023)

Изображение Вычислите:а) 1/2 + 1/5; в) 3/5 + 2/17; д) 5/7 + 0; ж) 1/2 - 1/13; и) 5/7 - 2/9; л) 4/7 + 4/5;б) 1/21 + 1/7; г) 1/7 + 7/9; е) 2/3 - 2/5; з) 3/5 -...

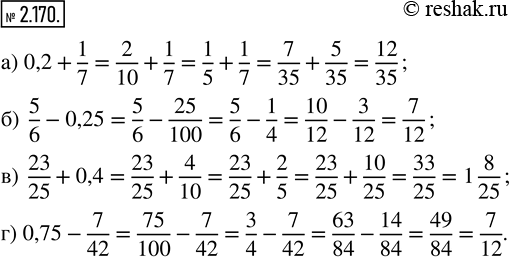
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

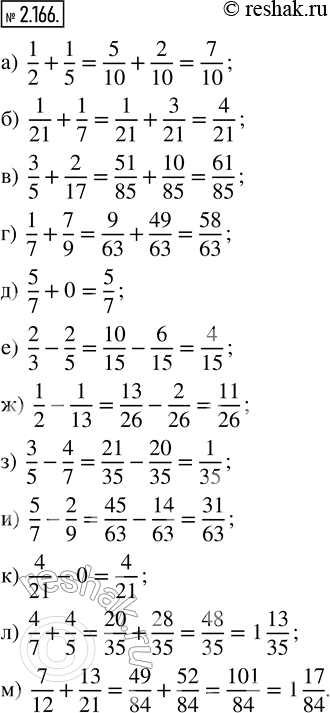
Решение #5 (Учебник 2021)

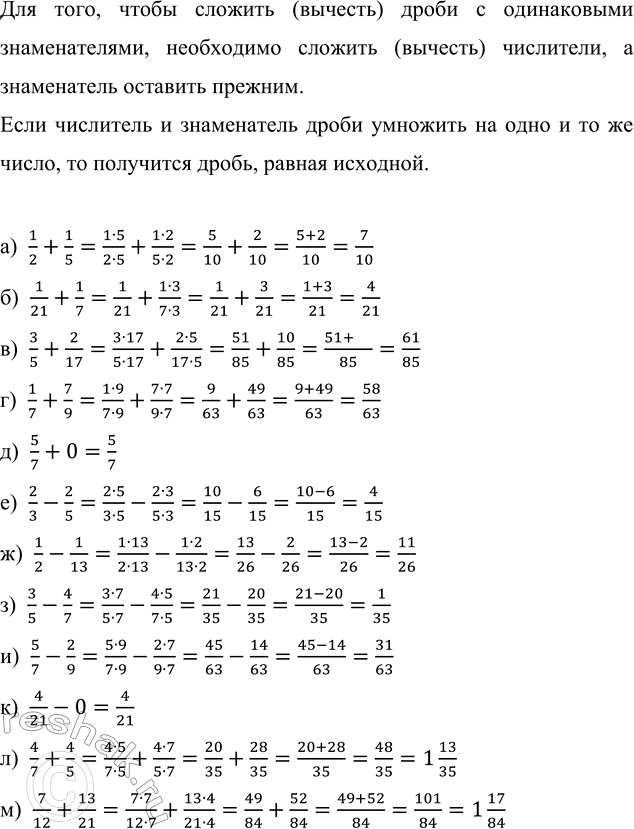
Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:

Представьте десятичную дробь в виде обыкновенной и вычислите:

а) 0,2 + 1/7; б) 5/6 - 0,25; в) 23/25 + 0,4; г) 0,75 - 7/42.

Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.

Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.

а) При переводе десятичной дроби, например, 0,2 в обыкновенную, в числителе дроби записывают число, стоящее после запятой, а в знаменателе 1 и столько нулей, сколько знаков стоит после запятой в десятичной дроби 0,2 (один знак).

0,2=2/10

Дробь 2/10 можно сократить на 2.

2/10=(1•2)/(5•2)=1/5

Для того, чтобы теперь сложить дроби с различными знаменателями, необходимо привести их к наименьшему общему знаменателю.

0,2+1/7=1/5+1/7=(1•7)/(5•7)+(1•5)/(7•5)=7/35+5/35=(7+5)/35=12/35

б) При переводе десятичной дроби 0,25 в обыкновенную, в числителе дроби записывают число, стоящее после запятой (25), а в знаменателе 1 и столько нулей, сколько знаков стоит после запятой в десятичной дроби 0,25 (два знака).

0,25=25/100

Дробь 25/100 можно сократить на 25.

25/100=(1•25)/(4•25)=1/4

Для того, чтобы теперь вычесть дроби с различными знаменателями, необходимо привести их к наименьшему общему знаменателю.

5/6-0,25=5/6-1/4=(5•2)/(6•2)-(1•3)/(4•3)=10/12-3/12=(10-3)/12=7/12

в) При переводе десятичной дроби 0,4 в обыкновенную, в числителе дроби записывают число, стоящее после запятой (4), а в знаменателе 1 и столько нулей, сколько знаков стоит после запятой в десятичной дроби 0,4 (один знак).

0,4=4/10

Дробь 4/10 можно сократить на 2.

4/10=(2•2)/(5•2)=2/5

23/25+0,4=23/25+2/5=23/25+(2•5)/(5•5)=23/25+10/25=(23+10)/25=33/25

Дробь 33/25 - неправильная, выделим целую часть.

(33:25=1 целая,в остатке 8).

33/25=1 8/25

г) При переводе десятичной дроби 0,75 в обыкновенную, в числителе дроби записывают число, стоящее после запятой (75), а в знаменателе 1 и столько нулей, сколько знаков стоит после запятой в десятичной дроби 0,75 (два знака).

0,75=75/100

Дробь 75/100 можно сократить на 25.

75/100=(3•25)/(4•25)=3/4

Дробь 7/42 можно сократить на 7.

7/42=(1•7)/(6•7)=1/6

0,75-7/42=3/4-1/6=(3•3)/(4•3)-(1•2)/(6•2)=9/12-2/12=(9-2)/12=7/12

Вычислите:

а) 1/2 + 1/5; в) 3/5 + 2/17; д) 5/7 + 0; ж) 1/2 - 1/13; и) 5/7 - 2/9; л) 4/7 + 4/5;

б) 1/21 + 1/7; г) 1/7 + 7/9; е) 2/3 - 2/5; з) 3/5 - 4/7; к) 4/21 - 0; м) 7/12 + 13/21.

Для того, чтобы сложить (вычесть) дроби с одинаковыми знаменателями, необходимо сложить (вычесть) числители, а знаменатель оставить прежним.

Если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная исходной.

а) 1/2+1/5=(1•5)/(2•5)+(1•2)/(5•2)=5/10+2/10=(5+2)/10=7/10