Упр.103 Задачи повышенной сложности ГДЗ Колмогоров 10-11 класс (Алгебра)
Решение #1
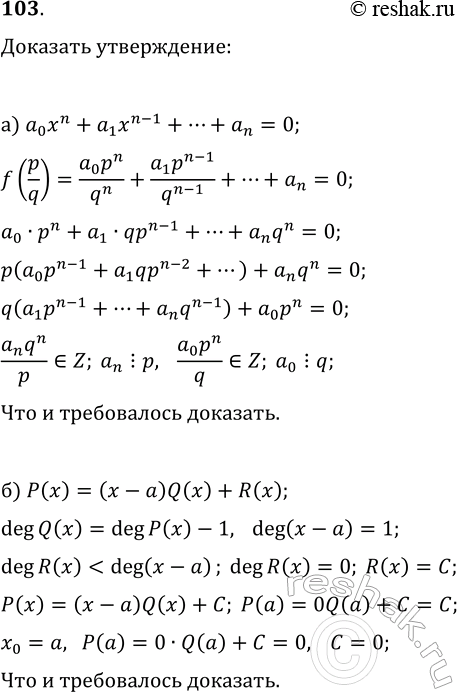
Рассмотрим вариант решения задания из учебника Колмогоров, Абрамов, Дудницын 10 класс, Просвещение:
103. Докажите, что: а) если x_0=p/1 — несократимая дробь, являющаяся корнем уравнения a_0x^n+a_1x^(n-1)+...+a_n=0 с целыми коэффициентами, то р — делитель a_n, a q — делитель a_0; б) остаток от деления многочлена Р(х) на одночлен (х-а) равен значению этого многочлена в точке а (в частности, если а — корень многочлена Р(х), то этот многочлен делится на (х-а) без остатка).
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением